Signalverarbeitung: Filter mit exponentiell gleitendem Durchschnitt (EMA)

Im Blog Einführung in die Signalverarbeitung haben wir bereits zwei Klassen von Filtern kennengelernt: „Endliche Impulsantwort (FIR)“ und „unendliche Impulsantwort (IIR)“. Wir haben gesehen, dass der gleitende Mittelwertfilter sowohl in einer FIR- als auch in einer IIR-Form ausgedrückt werden kann, aber welche Vorteile hat der eine gegenüber dem anderen?

Betrachtet man das Beispiel aus meinem letzten Blog, so hat der erweiterte FIR-Filter die Form:

y[5] = (x[5]+x[4]+x[3]+x[2]+x[1]+x[0])/5,

Hier sehen wir, was wir benötigen:

1. 5 Multiplikations- und
2. 4 Summationsoperationen.

Multiplikationsoperationen sind besonders rechenintensiv. Wenn wir uns also die IIR-Formel noch einmal ansehen, sehen wir, dass sie weniger erfordert:

1. 3 Multiplikations- und
2. 2 Summationsoperationen

y[6]=(x[6]+y[5]-x[1])/5

Dies reduziert die Rechenarbeit erheblich! Dies ist gut für eingebettete Geräte wie Mikrocontroller, da sie bei jedem diskreten Zeitschritt weniger Ressourcen für die Durchführung von Berechnungen benötigen.

Wenn ich zum Beispiel die Python-Funktion „time.time“ für das 11-Punkte-Filter mit gleitendem Mittelwert in FIR- und IIR-Form verwende, erhalte ich bei gleichbleibenden Parametern (Fenstergröße, Abtastrate, Abtastumfang usw.) die folgenden Laufzeitwerte: 51 ms, 27 ms.

Beispiel eines zeitdiskreten IIR-Filters

Nachdem wir nun eine Vorstellung davon haben, warum IIR-Filter auf Mikrocontrollern besser funktionieren, wollen wir uns ein Beispielprojekt mit einem Arduino UNO und einer Trägheitsmesseinheit (IMU) MPU6050 von DFRobot ansehen (Abbildung 1). Wir werden den Filter des exponentiell gleitenden Durchschnitts (EMA) auf die IMU-Daten anwenden, um die Unterschiede zwischen rohen und geglätteten Daten zu erkennen.

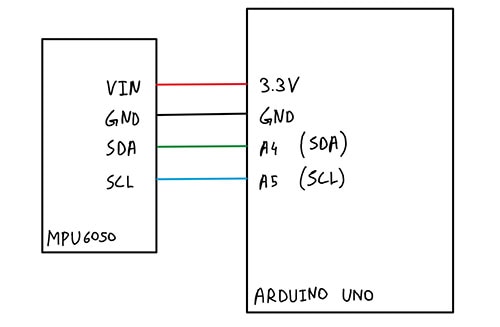Abbildung 1: Blockdiagramm der Verbindung zwischen der MPU6050 und dem Arduino Uno. (Bildquelle: Mustahsin Zarif)

Abbildung 2: Verbindung zwischen der MPU6050 und dem Arduino Uno. (Bildquelle: Mustahsin Zarif)

Der Filter für den exponentiell gleitenden Durchschnitt hat die rekursive Form:

y[n] = α*x[n] + (1- α)*y[n-1]

Es ist rekursiv, weil jede aktuelle Ausgabe, die wir messen, auch von den vorherigen Ausgaben abhängt, d. h. das System hat ein Gedächtnis.

Die Konstante alpha () legt fest, wie stark die aktuelle Eingabe im Vergleich zu den vorherigen Ausgaben gewichtet werden soll. Zur Verdeutlichung erweitern wir die Gleichung:

y[n] = α*x[n] + (1- α )*(α*x[n-1]+(1-α)*y[n-2])

y[n] = α*x[n] + (1- α )*x[n-1]+α*(1-α)2*x[n-2])+ ...

y[n] = k=0nα*(1-α)k*x[n-k]

Es zeigt sich, dass je größer das Alpha ist, desto stärker wirkt sich der aktuelle Input auf den aktuellen Output aus. Das ist gut, denn wenn sich das System weiterentwickelt, sind Werte, die weit in der Vergangenheit liegen, nicht so repräsentativ für das aktuelle System. Andererseits wäre es schlecht, wenn sich das System plötzlich und kurzzeitig vom Normalzustand abhebt; in diesem Fall möchten wir, dass unsere Ausgabe dem Trend folgt, dem die vorherigen Ausgaben gefolgt sind.

Sehen wir uns nun an, wie der Code für einen EMA-Filter für die MPU6050 funktionieren würde.

EMA-Filtercode:

Kopieren#include <wire.h>
#include <mpu6050.h>

MPU6050 mpu;

#define BUFFER_SIZE 11  // Window size

float accelXBuffer[BUFFER_SIZE];
float accelYBuffer[BUFFER_SIZE];
float accelZBuffer[BUFFER_SIZE];
int bufferCount = 0;  

void setup() {
  Serial.begin(115200);
  Wire.begin();

  mpu.initialize();

  if (!mpu.testConnection()) {
    Serial.println("MPU6050 connection failed!");
    while (1);
  }

  int16_t ax, ay, az;
  for (int i = 0; i < BUFFER_SIZE; i++) {
    mpu.getMotion6(&ax, &ay, &az, NULL, NULL, NULL);
    accelXBuffer[i] = ax / 16384.0;
    accelYBuffer[i] = ay / 16384.0;
    accelZBuffer[i] = az / 16384.0;
  }
  bufferCount = BUFFER_SIZE;
}

void loop() {
  int16_t accelX, accelY, accelZ;

  mpu.getMotion6(&accelX, &accelY, &accelZ, NULL, NULL, NULL);

  float accelX_float = accelX / 16384.0;
  float accelY_float = accelY / 16384.0;
  float accelZ_float = accelZ / 16384.0;

  if (bufferCount < BUFFER_SIZE) {
    accelXBuffer[bufferCount] = accelX_float;
    accelYBuffer[bufferCount] = accelY_float;
    accelZBuffer[bufferCount] = accelZ_float;
    bufferCount++;
  } else {
    for (int i = 1; i < BUFFER_SIZE; i++) {
      accelXBuffer[i - 1] = accelXBuffer[i];
      accelYBuffer[i - 1] = accelYBuffer[i];
      accelZBuffer[i - 1] = accelZBuffer[i];
    }
    accelXBuffer[BUFFER_SIZE - 1] = accelX_float;
    accelYBuffer[BUFFER_SIZE - 1] = accelY_float;
    accelZBuffer[BUFFER_SIZE - 1] = accelZ_float;
  }

//calculate EMA using acceleration values stored in buffer
  float emaAccelX = accelXBuffer[0];
  float emaAccelY = accelYBuffer[0];
  float emaAccelZ = accelZBuffer[0];
  float alpha = 0.2;

  for (int i = 1; i < bufferCount; i++) {
    emaAccelX = alpha * accelXBuffer[i] + (1 - alpha) * emaAccelX;
    emaAccelY = alpha * accelYBuffer[i] + (1 - alpha) * emaAccelY;
    emaAccelZ = alpha * accelZBuffer[i] + (1 - alpha) * emaAccelZ;
  }

  Serial.print(accelX_float); Serial.print(",");
  Serial.print(accelY_float); Serial.print(",");
  Serial.print(accelZ_float); Serial.print(",");
  Serial.print(emaAccelX); Serial.print(",");
  Serial.print(emaAccelY); Serial.print(",");
  Serial.println(emaAccelZ);

  delay(100);
}
</mpu6050.h></wire.h>

Wenn wir diesen Code ausführen und den seriellen Plotter überprüfen, können wir grobe und glatte Linien in Paaren für Beschleunigungen in der x-, y- und z-Achse sehen, wenn wir eine Fenstergröße von 11 und einen Alphawert von 0,2 verwenden (Abbildung 3 bis 5).

Abbildung 3: Rohe und gefilterte Beschleunigungswerte in x-Richtung. (Bildquelle: Mustahsin Zarif)

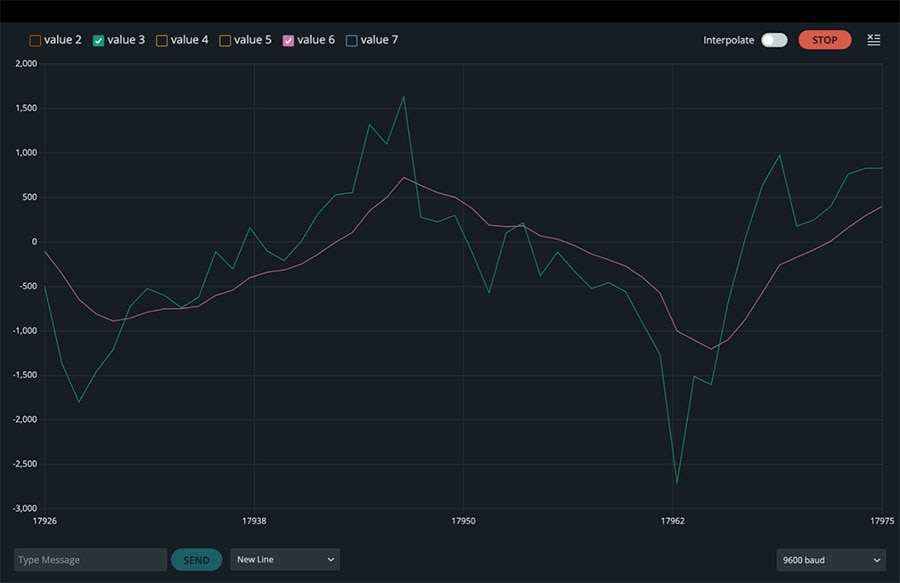Abbildung 4: Rohe und gefilterte Beschleunigungswerte in y-Richtung. (Bildquelle: Mustahsin Zarif)

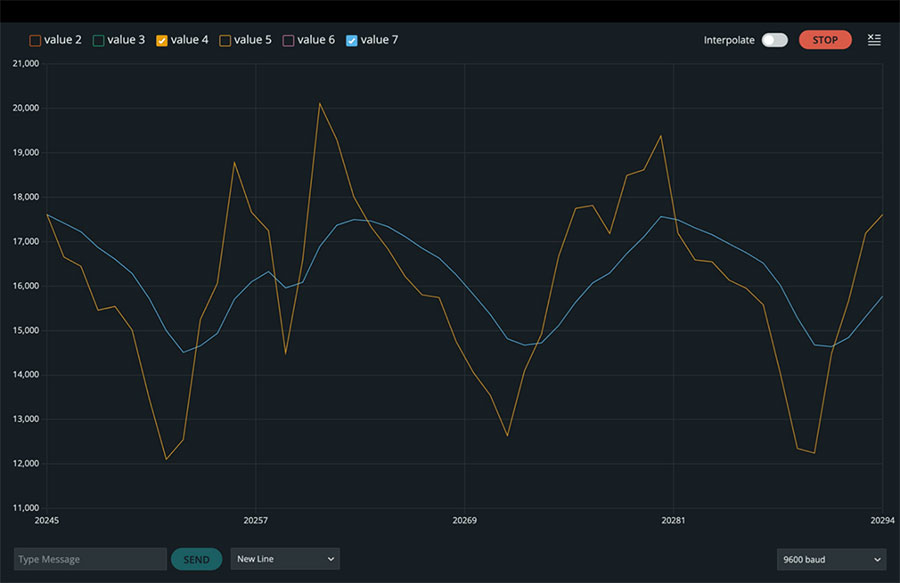Abbildung 5: Rohe und gefilterte Beschleunigungswerte in z-Richtung. (Bildquelle: Mustahsin Zarif)

Den Code einen Schritt intelligenter machen

Wir haben nun eine Vorstellung davon, dass IIR-Filter im Vergleich zu FIR-Filtern besser für Steuerungen geeignet sind, da wesentlich weniger Summations- und Multiplikationsberechnungen erforderlich sind. Wenn wir diesen Code implementieren, sind Addition und Multiplikation jedoch nicht die einzigen Berechnungen, die durchgeführt werden: Wir müssen die Stichproben jedes Mal verschieben, wenn eine neue Zeitstichprobe eintrifft, und dieser Prozess erfordert unter der Haube Rechenleistung. Daher können wir, anstatt alle Proben bei jedem Abtastzeitintervall zu verschieben, die Hilfe von zirkulären Puffern nutzen.

Wir gehen folgendermaßen vor: Wir haben einen Zeiger, der den Index der eingegangenen Datenprobe speichert. Dann zeigt der Zeiger jedes Mal, wenn er auf das letzte Element des Puffers zeigt, beim nächsten Schritt auf das erste Element des Puffers, und die neuen Daten ersetzen die Daten, die zuvor hier gespeichert waren, da dies nun die ältesten Daten sind, die wir nicht mehr benötigen (Abbildung 6). Folglich können wir mit dieser Methode die älteste Probe im Puffer verfolgen und diese ersetzen, ohne jedes Mal Proben verschieben zu müssen, um die neuen Daten in das letzte Element des Arrays zu setzen.

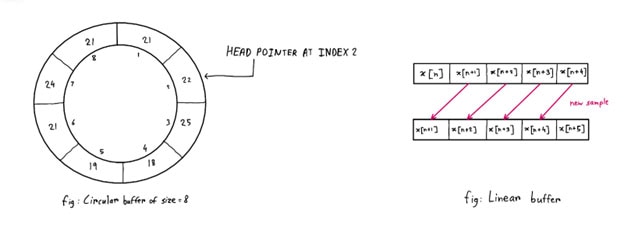Abbildung 6: Beispielhafte Darstellung eines Ringspeichers. (Bildquelle: Mustahsin Zarif)

So sieht der Code für eine EMA-Filter-Implementierung mit zirkulären Puffern aus. Können Sie dies für ein Gyroskop anstelle eines Beschleunigungsmessers durchführen? Spielen Sie auch mit den Koeffizienten!

Code für einen EMA-Filter unter Verwendung eines zirkulären Puffers:

Kopieren#include <wire.h>

#include <mpu6050.h>

MPU6050 mpu;

#define BUFFER_SIZE 11  // Window size

float accelXBuffer[BUFFER_SIZE];

float accelYBuffer[BUFFER_SIZE];

float accelZBuffer[BUFFER_SIZE];

int bufferIndex = 0;  

void setup() {

  Serial.begin(115200);

  Wire.begin();
 

  mpu.initialize();


  if (!mpu.testConnection()) {

    Serial.println("MPU6050 connection failed!");

    while (1);

  }

  int16_t ax, ay, az;

  for (int i = 0; i < BUFFER_SIZE; i++) {

    mpu.getMotion6(&ax, &ay, &az, NULL, NULL, NULL);

    accelXBuffer[i] = ax / 16384.0;

    accelYBuffer[i] = ay / 16384.0;

    accelZBuffer[i] = az / 16384.0;

  }

}

void loop() {

  int16_t accelX, accelY, accelZ;

  mpu.getMotion6(&accelX, &accelY, &accelZ, NULL, NULL, NULL);

  float accelX_float = accelX / 16384.0;

  float accelY_float = accelY / 16384.0;

  float accelZ_float = accelZ / 16384.0;

  accelXBuffer[bufferIndex] = accelX_float;

  accelYBuffer[bufferIndex] = accelY_float;

  accelZBuffer[bufferIndex] = accelZ_float;

  bufferIndex = (bufferIndex + 1) % BUFFER_SIZE; //circular buffer implementation 

  float emaAccelX = accelXBuffer[bufferIndex];

  float emaAccelY = accelYBuffer[bufferIndex];

  float emaAccelZ = accelZBuffer[bufferIndex];

  float alpha = 0.2;

  for (int i = 1; i < BUFFER_SIZE; i++) {

    int index = (bufferIndex + i) % BUFFER_SIZE;

    emaAccelX = alpha  accelXBuffer[index] + (1 - alpha)  emaAccelX;

    emaAccelY = alpha  accelYBuffer[index] + (1 - alpha)  emaAccelY;

    emaAccelZ = alpha  accelZBuffer[index] + (1 - alpha)  emaAccelZ;

  }

  Serial.print(accelX_float); Serial.print(",");

  Serial.print(emaAccelX); Serial.print(",");

  Serial.print(accelY_float); Serial.print(",");

  Serial.print(emaAccelY); Serial.print(",");

  Serial.print(accelZ_float); Serial.print(",");

  Serial.println(emaAccelZ);

  delay(100);

}
</mpu6050.h></wire.h>

Zusammenfassung

In diesem Blog haben wir den Unterschied zwischen IIR- und FIR-Filtern erörtert, wobei der Schwerpunkt auf ihrer Berechnungseffizienz lag. Anhand eines kleinen Beispiels für die Verringerung der Anzahl der erforderlichen Operationen von FIR zu IIR können wir uns vorstellen, wie effizient IIR-Filter sein werden, wenn Anwendungen skaliert werden, was für Echtzeitanwendungen mit begrenzter Hardwareleistung wichtig ist.

Wir haben uns auch ein Beispielprojekt mit einem Arduino Uno und einer MPU6050-IMU angesehen, bei dem wir einen exponentiell gleitenden Mittelwertfilter eingesetzt haben, um das Rauschen in den Sensordaten zu reduzieren und gleichzeitig das zugrunde liegende Signalverhalten zu erfassen. Schließlich haben wir im Interesse der Effizienz auch ein Beispiel für intelligenteren Code gesehen, bei dem zirkuläre Puffer verwendet werden, anstatt die Daten in jedem Zeitintervall zu verschieben.

Im nächsten Blog werden wir die FPGA-Funktionalität von Red Pitaya nutzen, um eine digitale Schaltung für einen FIR-Filter mit 4 Abgriffen zu implementieren!